Problem Statement: To economically design a carton box to pack 20 half-litre pouches.

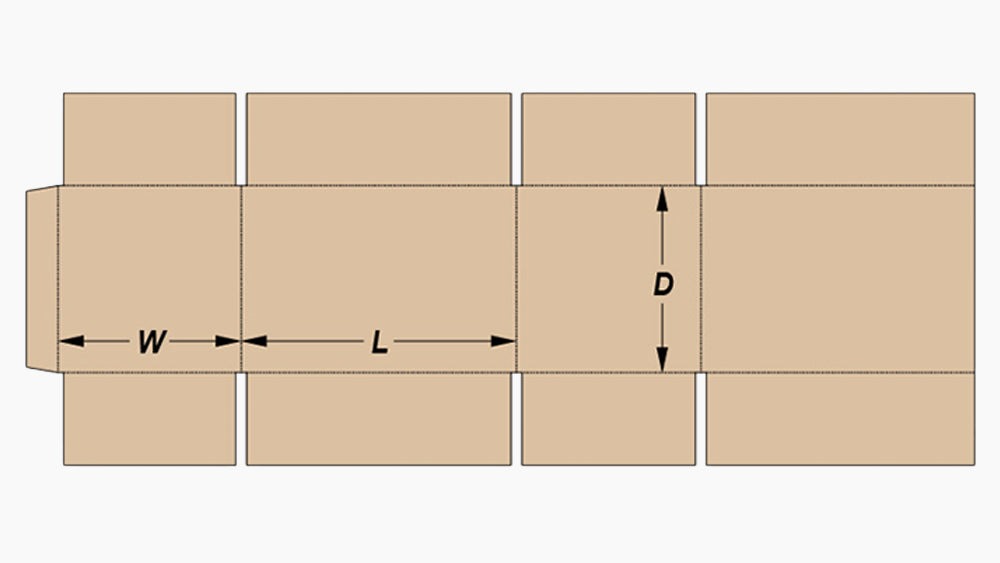
Regular Slotted Carton

The carton box is formed from a Regular Slotted Carton (RSC). The image shows how cardboard is cut to form the carton box.

Solution

If l is the length, b the breadth, and h the height of the formed carton box, then the area of the cardboard used is:

Area = 2 × (l + b) × (b + h)

The cost of the carton box is directly proportional to the area of the cardboard used. Therefore, the goal is to minimize the area of the cardboard for a given volume.

Objective: Minimize 2 × (l + b) × (b + h), given that l × b × h = V, a constant.

Note: Ideally, the surface area of a cuboid is 2(lb + bh + lh), but here there's an extra 2b² area. This becomes the inner flaps of the box, which provide additional strength. Cutting the cardboard this way is also simpler, as it forms a rectangle of dimensions 2(l + b) by (b + h).

Although a cube provides the minimum surface area for a given volume, that’s not directly applicable here due to the extra flap area.

Let F(l, b, h) = (l + b)(b + h) = lb + lh + b² + bh (ignoring the factor 2 for simplification).

Since l × b × h = V, we substitute l = V / (b × h) into the equation:

F(b, h) = V/h + V/b + b² + bh

Now, differentiate with respect to h:

F_h(b, h) = -V/h² + b

Setting it to zero gives: b = V / h²

Since l = V / (b × h) and substituting the above value, we get: l = h

So now, V = b × h² and Area = 2 × (h + b)². Minimizing (h + b) will minimize the area.

Let F(b, h) = h + b, and since b = V / h²,

F(h) = h + V / h²

Differentiating:

F’(h) = 1 – 2V / h³

Setting it to zero: h³ = 2V → h = (2V)^1/3

Now, b = V / h² = (V / 4)^1/3 and l = h.

Optimal dimensions:
l = (2V)^1/3,
b = (V/4)^1/3,
h = (2V)^1/3

In our case, for 20 pouches of 500 ml, the volume is 10 litres. Adding a 25% allowance for pouch flexibility and shape irregularities, we get a required carton volume of 12.5 litres or 12,500 cm³.

Optimal dimensions for V = 12,500 cm³:
l = 29.24 cm,
b = 14.62 cm,
h = 29.24 cm

Comparison

Currently, we use a standard-sized carton for both half-litre and one-litre pouches. We’re limited by low order volumes.

Existing box dimensions:
l = 32 cm, b = 19 cm, h = 21 cm
Volume = 12,768 cm³
Area = 4,080 cm²

Optimized box dimensions for same volume:
l = 29.45 cm, b = 14.72 cm, h = 29.45 cm
Area = 3,902 cm²

Result: The optimized design is 4.35% more efficient in terms of cardboard area. While it may seem minor, carton boxes are used in large quantities, and savings add up significantly over time.

At Cocoguru, we carefully analyze the cost of each item to minimize expenses without compromising customer value.

Cutting Costs is not about Cutting Corners — it’s about smart Value Engineering.